Vic's粒子

大問1

(1)

これは、部分分数分解と言われる計算の工夫を使って解く問題です。

北嶺中では、過去に3回出題されています。

 

平成3年度　大問1(1)

 

平成17年度　大問1(4)

 

平成24年度　大問1(2)

 

令和2年度の問題では、次のように分数を分解できることを利用します。

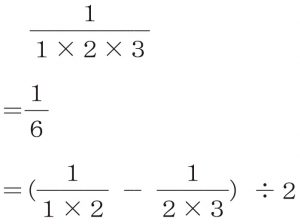
上記の式を利用すると、次のように解くことができます。

 

(2)

｛1.001＋(1.2×1.2×1.2＋0.001)｝÷0.91－(10－0.01)÷3.7

＝ (1.001＋    1.728    ＋0.001)  ÷0.91－   9.99   ÷3.7

＝ 　　　　　2.73 　　　　　÷0.91－　　　2.7

＝　　　　　　　3 　　　　　　　－　　　2.7

＝　0.3

 

ポイント①

1729は、ラマヌジャン数と言います。

数学者ハーディ・ラマヌジャンの逸話はさておき、

1729は2通りの立方数(5×5×5＝125のように、同じ数を3回かけた数)と立方数との和で

表すことのできる最小の整数です。

1729

＝(1×1×1)＋(12×12×12)

＝(9×9×9)＋(10×10×10)

以上の話を知っていれば、1.2×1.2×1.2＋0.001を見た瞬間に

1.2×1.2×1.2＋0.1×0.1×0.1＝(12×12×12＋1×1×1)÷1000

で「ラマヌジャン数だから1729」と分かります。

これは、北嶺からの

「算数や数学に興味を持ち、いろいろな本を日ごろから読むようにしましょう」

というメッセージですね。

 

ポイント②

9.99÷3.7の部分について、

「111＝37×3」というかけ算の組み合わせは、

ときどき出てくるので覚えておくと便利です。

9.99÷3.7

＝9×1.11÷3.7

＝9×0.3

＝2.7

となります。過去にも、

平成26年度　大問1(3)　(370.37÷9.1－99.9×７÷27)÷3.7

で出題されています。

 

(3)

 

 

(4)

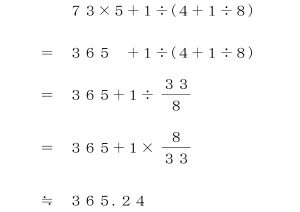
365という数字から、365日という1年の日数が連想されます。

式の後半にある「1÷(4＋1÷8)」の部分も、

うるう年で増える1日を、だいたい4年で割っているという印象を受験生に与えます。

だいたい4年、とあいまいに書いたのは、西暦について

4で割れる年(例：西暦2020年)は、うるう年である。

上のうち、100で割れる年(例：西暦2100年)は、うるう年でない。

上のうち、400で割れる年(例：西暦2400年)は、うるう年である。

という規則があるからです。

この規則については、立命館慶祥中の入試問題で出題されています。

 

大問2

(1)

文章を、次の表のようにまとめました。

できるだけ多くBセットで頼んだ方が、安くなる金額が大きくなります。

よって、まず、ポテトの6個に合わせてBを6セット注文します。

あと、ハンバーガーが8－6＝2(個)、ジュースが9－6＝3(杯)必要なので、

Aを2セット、ジュースを1杯注文します。

Aは、ひとセットにつき30円安くなり、Bはひとセットにつき50円安くなります。

よって、合計で30×2＋50×6＝360(円)安くなります。

 

(2)

三角形BDFについて、図1のように正六角形を分けると、

三角形BDFは正六角形の1/2になります。

四角形ACDFについて、図2のように正六角形を分けると、

四角形ACDFは正六角形の2/3になります。

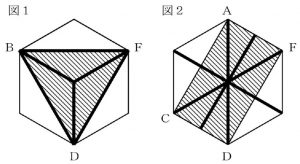
1/2 ÷ 2/3 ＝ 3/4(倍)

より、三角形BDFは四角形ACDFの3/4倍です。

 

(3)

ABCの学校を合わせて、150＋100＋200＝450(人)の児童がいます。

平均点が30.6点なので、全児童の合計点は、30.6×450＝13770(点)です。

 

このうち、Aでは(8＋7＋9＋7)×150＝4650(点)、

Cでは(8＋7＋7＋8)×200＝6000(点)をとっています。

分かる範囲では、Bでは(7＋8＋8)×100＝2300(点)をとっています。

よって、分かる範囲の合計点は、4650＋6000＋2300＝12950(点)です。

 

全体との差である13770－12950＝820(点)は、[ア]の点数かける100人です。

よって、[ア]＝820÷100＝8.2となります。

 

(4)

下図のように、三角形COEと三角形AOFとは、

1つの辺の長さとその両端の角の大きさがそれぞれ等しいので、

合同だと分かります。

よって、この２つの三角形の面積は、同じです。

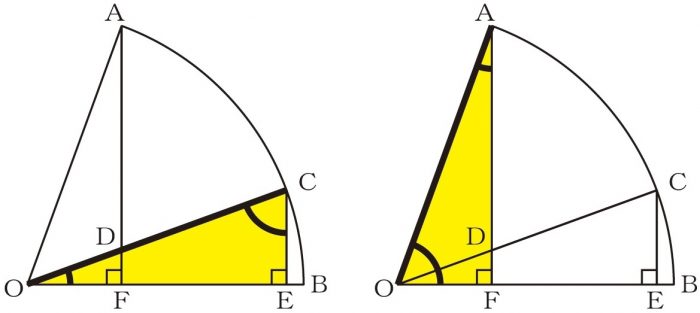
この2つの三角形から、

三角形DOFをそれぞれ引いた台形CDFEと三角形AODの面積も、

やはり同じになります。

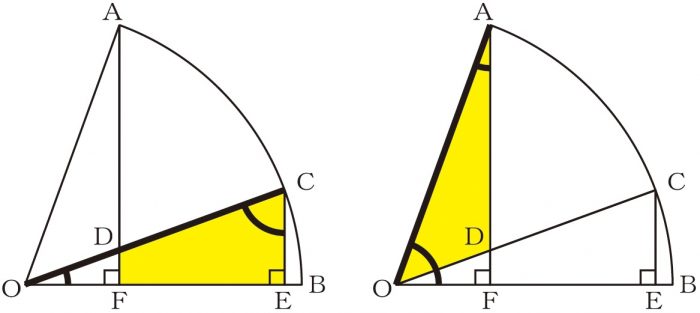
よって、下図のように、求めるべき斜線部分の面積は

扇形AODと等しいことが分かります。

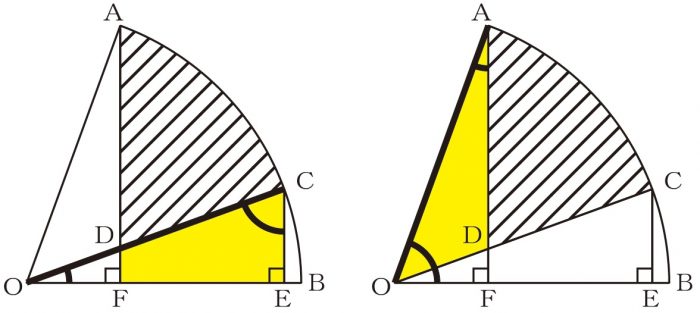
10×10×3.14×50/360≒43.61(㎠)

 

(5)

まず、A家からの距離を確認します。

A家からB家までは1200－700＝500(m)、

A家からC家までは1200－70＝1130(m)です。

 

次に、AがC家まで行くのにかかる時間は1130÷60＝18と5/6より、

18分50秒です。

よって、7時55分に出発したAが、C家の前まで来るのは8時13分50秒です。

下図の赤線は、Aの進んだ時刻と距離を表しています。

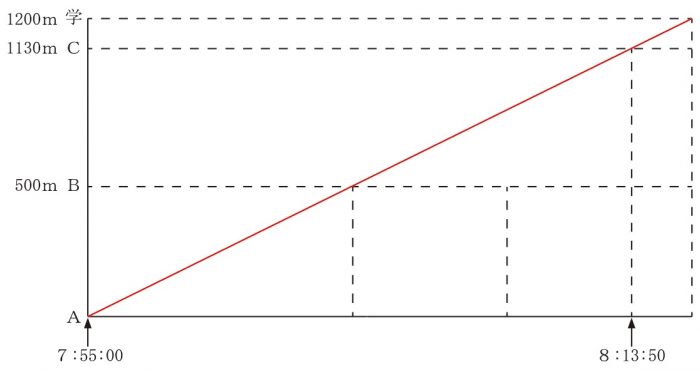
さて、AがB家の前に来てから、C家の前に来るまでに、

BはAと出会わなければなりません。

このとき、Bの進んだ時刻と距離は、

下図の青線のどれでもよいことになります。

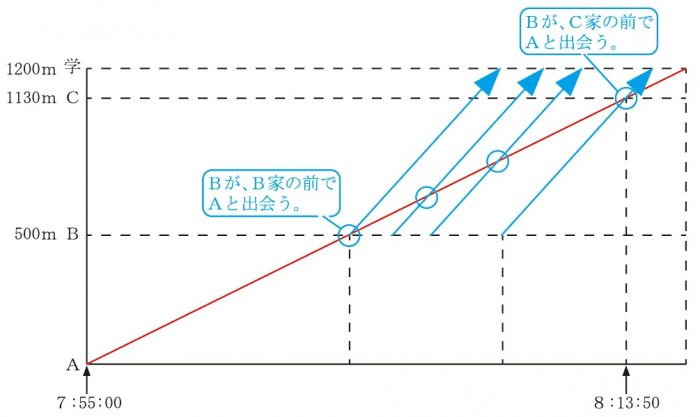
よって、Bが家を出る時刻は、下図の緑色でマルをつけたところになります。

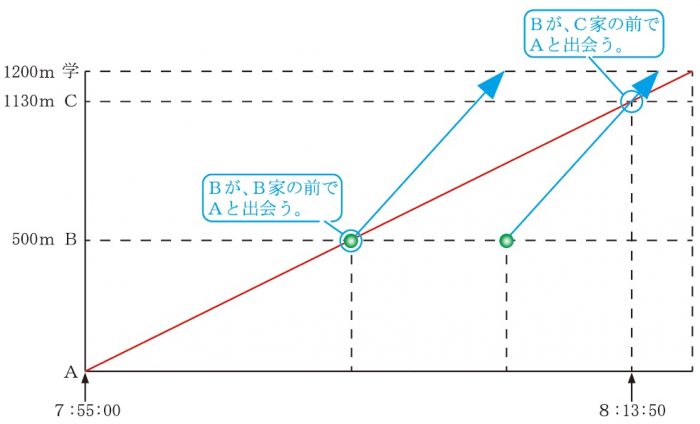
Bが、B家の前でAと出会う時刻は、AがB家の前に来たときです。

7時55分から500÷60＝8と1/3(分)後の8時3分20秒です。

また、Bは、B家とC家との間の1130－500＝630(ｍ)を進むのに、

630÷75＝8.4分(8分24秒)かかります。

8時13分50秒に、BがC家の前でAに出会うためには、

8時13分50秒より8分24秒前の8時5分26秒に

BはB家を出発することになります。

以上より、Bは、8時3分20秒から8時5分26秒までに

家を出なければならないことになります。